https://www.acmicpc.net/problem/1520
💡 해결방법
DFS + DP메모제이션
DFS 만으로 풀면 시간초과or메모리초과
DP 만으로 풀면 메모리초과
처음엔 상하좌우가 아니라 [좌,우,아래]로만 움직일 수 있는 줄 알고 O(N^3) 풀이를 준비했던,,
(0,0)에서 (r-1, c-1) 위치로 이동하는 경우의 수를 구하는 문제이다.
이동 조건은 상하좌우 다 되고, 대신 grid의 현재위치의 높이가 이동하려는 위치의 높이보다 높아야 된다.
처음 접근했던 방법이다.
목적지(10)에서 목적지로 가는 방법은 0개라고 가정하고, 목적지에서 상하좌우에 자기 높이보다 높은 숫자로 이동하면서 {현재 방법 + 1}로 두는 방법으로 접근을 했다. 하지만 결국 그냥 dfs로 푸는 것과 별 차이가 없었다.
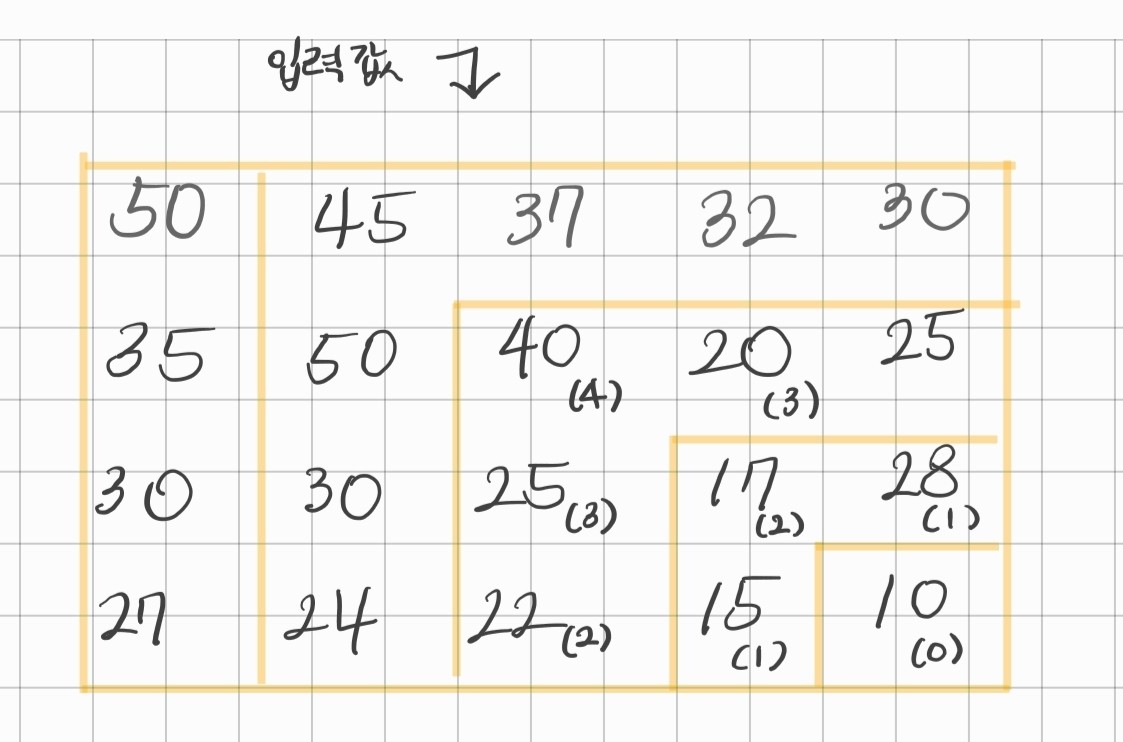
아싸리 그냥 이번엔 dfs로 완전 가보자. 하고 그린 그림이다.
막상 그림을 그리다보니 32에서 20과 30에서 한 번씩 거쳐가는 상황을 잘 표현할 수 있겠다 싶었다.
그 방법이 dp 테이블을 이용한 것이다.

생각난 김에 밑에 코드도 후다닥 썼다.
물론 recursion 하려는 좌표가 범위 안에 들어오는지, 이미 탐색한 곳인지, 더 높은 숫자 아닌지 등 따질 것이 있다.
이렇게 핵심 아이디어를 접하고 코드로 구현했다.
🧾코드
# 1520 내리막길
import sys
sys.setrecursionlimit(10**5)
r, c = map(int, input().split())
grid = [list(map(int, input().split())) for _ in range(r)]
#북 동 남 서
dy, dx = [-1, 0, 1, 0], [0, 1, 0, -1]
dp = [[-1]*c for _ in range(r)]
def DFS(y, x):
if y == r-1 and x == c-1:
return 1
if dp[y][x] != -1:
return dp[y][x]
dp[y][x] = 0
for i in range(4):
ny, nx = y+dy[i], x+dx[i]
if 0<=ny<r and 0<=nx<c and grid[ny][nx] < grid[y][x]:
dp[y][x] += DFS(ny, nx)
return dp[y][x]
print(DFS(0, 0))코드 설명
if dp[y][x] != -1:
return dp[y][x]이미 탐색을 완료한 경우라면 그냥 그 위치에서 이동 경우의 수를 바로 가져온다. (굳이 똑같은 길로 탐색을 할 필요가 없다)
댓글