세그먼트 트리란?
세그먼트 트리는 구간의 정보를 알고 싶을 때 사용하는 트리입니다.
각 노드는 자식 노드의 정보를 연산한 값을 저장하고 있습니다. 이 특징으로 구간의 사칙연산, 최대·최솟값 등을 구할 때 자주 사용한다고 합니다.
개발자는 배열 혹은 리스트에서 부분의 합 정보를 알고 싶습니다. 그래서 선형 탐색으로 접근을 하고, 구간이 일치한다면 그 정보들을 하나하나 가져옵니다. 이것은 구현이 쉬우나, O(N)의 비용이 발생합니다.
세그먼트 트리의 노드는 부분의 정보를 저장하고 있습니다.
말단 노드(leaf node)에 접근하면, 배열의 원소 값과 일치합니다.
하지만 말단 노드의 부모 노드 부터는, 자식 노드의 정보를 합한(혹은 빼거나 곱하는 등) 값을 저장하고 있습니다.
그래서 필요한 구간의 노드를 찾아내면 원하는 정보를 빠르게 구할 수 있습니다.
공부를 하면서 저는 개인적으로 누적합과 배열의 장점을 하나씩 가져왔다고 생각했습니다.
구간의 합은 누적합을 이용해서도 빠르게 구할 수 있습니다.
정보의 수정은 배열에서 오히려 더 빠릅니다. 접근에 O(1) 비용밖에 들지 않으니까요.
하지만 정보의 수정이 자주 일어난다면, 누적합을 이용하기엔 시간적 비용이 크게 들겁니다.
당연히 구간의 합을 자주 구해야 한다면, 마찬가지로 배열도 큰 시간적 비용이 들겁니다.
그래서 이 두가지의 상황이(정보의 수정, 구간의 합을 접근해야 할 때) 자주 발생한다면, 당연히 세그먼트 트리를 이용해야 할 것입니다.
세그먼트 트리는 어떻게 만들지?
세그먼트 트리의 코드를 먼저 보겠습니다.
arr = [i for i in range(1, 11)]
tree = [0] * (len(arr) * 4)
def init_tree(start, end, current):
if (start == end):
tree[current] = arr[start]
return tree[current]
mid = (start + end) // 2
tree[current] = init_tree(start, mid, current*2) + init_tree(mid+1, end, current*2+1)
return tree[current]
init_tree(0, len(arr)-1, 1)tree의 size는 arr의 길이보다 크거나 같은 최소 제곱수의 2배가 맞다곤 하는데, arr의 길이의 4배로 해도 괜찮다고 합니다.
* 4배로 하는 이유를 위키독스-트리 만들기에서 그 이유를 시각적으로 잘 보이는 것 같아서 링크 남깁니다.

파란색이 init 함수를 따라 트리의 아래로 내려가는 모습이고
빨간색이 말단 노드에서 값을 저장하고, return 해주며 다시 트리의 위로 올라가면서 합을 저장하는 모습입니다.
구간의 합은 어떻게 구할까?
이제 트리를 구현했으니 '구간의 합은 어떻게 구할 수 있을까?' 하는 물음에서 끄적인 코드입니다.
# 내가 구현한 부분합 구하는 함수
def sol(start, end, idx, i, k):
if (i == k and start == end):
return tree[idx]
elif (start == i and end == k):
return tree[idx]
elif ((start > i and end < k) or (i > k)):
return 0
mid = (start + end) // 2
return sol(start, mid, idx*2, max(start, i), min(mid, k)) + sol(mid+1, end, idx*2 +1, max(mid+1, i), min(end,k))
print(f"4 ~ 7까지 부분합:", sol(0, len(arr)-1, 1, 4, 7))세세한 조건을 따져가니 위 조건식으로 완성했습니다.
'start-mid-end 로 접근 구간의 범위가 달리지므로, i와 k도 맞춰가야 할 것 같다'고 생각했습니다.
이러고 다른 코드와 비교해보니 약간의 차이가 있었습니다.
# 외부 사이트에서 구현되어 있는 부분합 함수
def interval(start, end, idx, i, j):
if (i<=start and end<=j):
return tree[idx]
elif (end < i or start > j):
return 0
mid = (start+end) //2
return interval(start, mid, idx*2, i, j) + interval(mid+1, end, idx*2 +1, i, j)
print(f"4 ~ 7까지 부분합:", interval(0, len(arr)-1, 1, 4, 7))
우선 조건식이 더 간결해지고 코드 가독성이 올라간 느낌입니다.
처음에는 저 조건식들이 이해하기 어려웠는데 손으로 그림을 그려가며 따라가니 이해하기 좋은 방법이 있더군요.

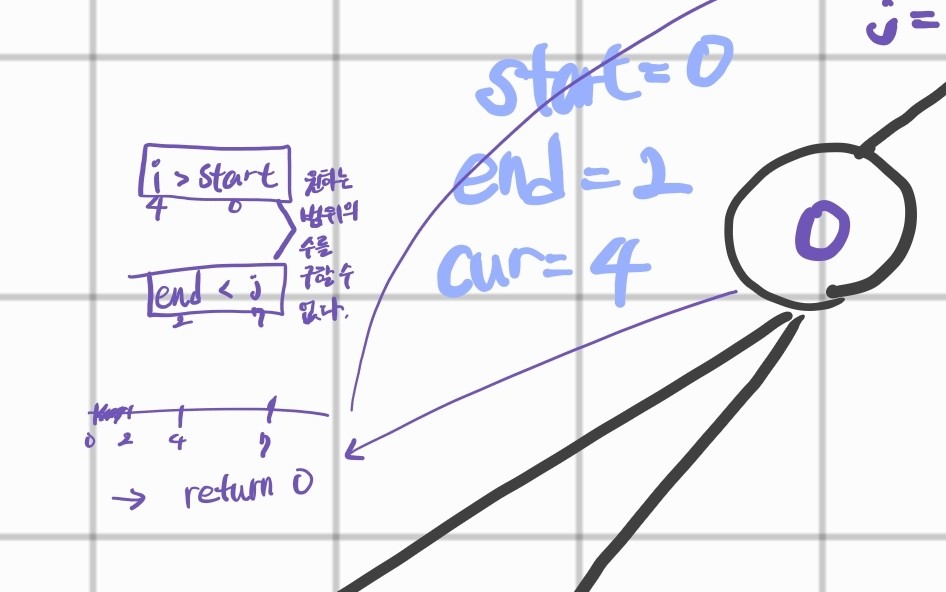
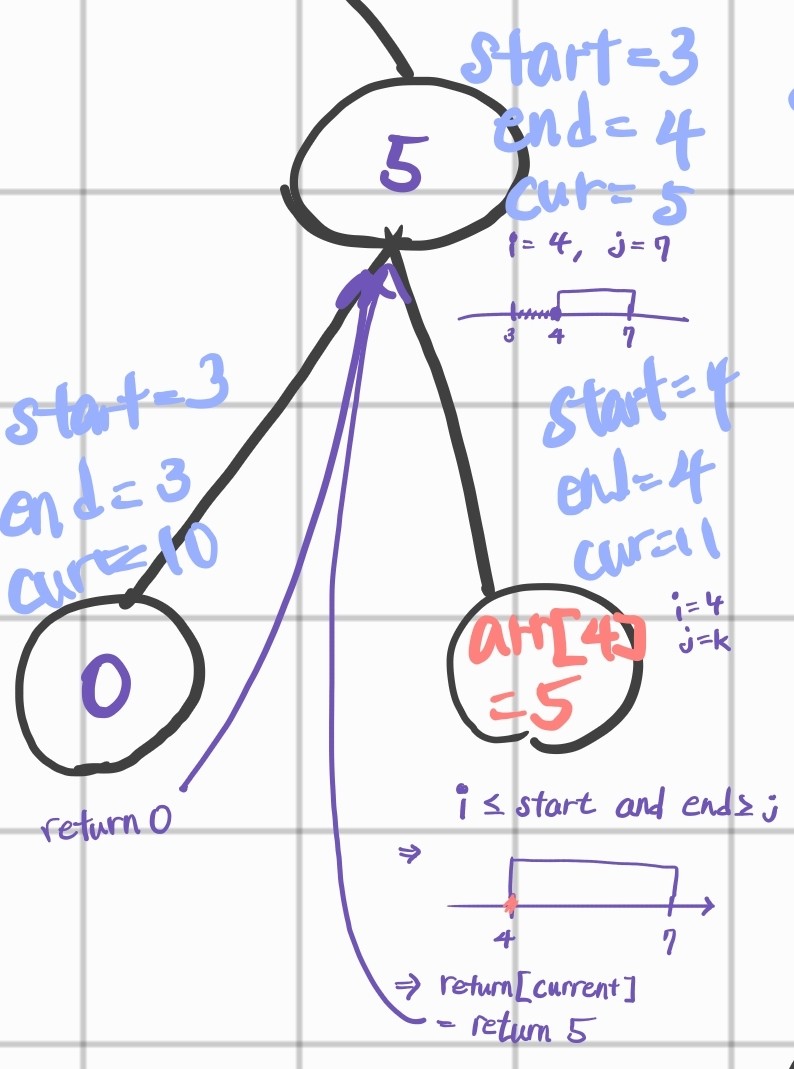
초등학교 · 중학교 때 배웠던 부등식 도식화가 이해하는 데에 큰 도움이 되었습니다. 이렇게 하니 범위 체크하는 것도 한 눈에 알아보기 편하고 이해도 잘 되고.. 왜 이렇게 조건식을 쓰는지 잘 알았더랬죠.
그럼 수정은 어떻게 하지?
# idx: tree의 index위치
# where: arr에서 수정하는 위치
# value: 수정하는 값
def modify(start, end, idx, where, value):
# 범위 바깥으로 나가면 종료
if (where < start or where > end):
return
# 수정
tree[idx] -= value
# 리프노드 까지 왔으면 종료
if (start == end):
return
mid = (start+end) //2
modify(start, mid, idx*2, where, value)
modify(mid+1, end, idx*2+1, where, value)
수정은 트리의 위에서부터 아래로 내려가면서 값을 갱신하면 됩니다.
그 이유는 변경하려는 값이 tree의 어느 위치(index)에 있는지 모르기 때문입니다.
'아니, 그러면 나는 arr의 6번째 인덱스 값을 100으로 바꿀건데. 그러면 트리의 리프노드부터 100으로 바뀌는거 아니냐?'
싶을 수도 있습니다. 제가 그랬거든요. 그래서 어떻게 하면 좋을지 고민을 해보니 답은 간단했습니다.
기존의 값(arr[6]==7 :true)과 바꾸려는 값(100)의 차이를 구해서 리프노드부터 내려가면서 그 차이만큼 더하거나 빼주면 갱신이 됩니다.
'더하거나 뺀다는 게 무슨 말이냐?' 싶을 수도 있습니다.
arr[6] - 100과
100 - arr[6]은 부호가 다릅니다.
말단 노드(tree에서 arr[6]이 위치하는 곳) 값이 7이니까. 100을 만드려면 93을 더해줘야 합니다. 여기서 93을 더해줘야 하는 것은 7이 위치한 노드뿐만 아니라 7의 모든 조상 노드들에도 93을 더해주면 내려가면서 갱신을 끝낼 수 있습니다.
'그래서 더하거나 뺀다는 게 대체 무슨 말인데? 다른 얘기잖아.' 하실 수도 있습니다.
여기부터 설명하겠습니다. 수정 메소드에서 만약 갱신 방법을 '+='로 했다면 '100 - arr[6] (=100 - 7= +93)' 으로, 반대로 '-='로 했다면 'arr[6]-100 (=7 - 100 = -93)' 으로 입력을 해줘야 합니다.
정리하자면 개발자가 갱신을 어떻게(+로 했느냐, -로) 했느냐를 주의깊게 보란 말이었습니다. 별건 아니지만 이런 사소한 것으로 함수가 완성되느냐, 안 되느냐가 갈리기 때문에 구현 할 때는 한 가지 방법으로 하는 것이 좋겠습니다.
'자료구조' 카테고리의 다른 글
| 중위표기식을 후위표기식으로 변환하기 (Java) (0) | 2025.04.12 |
|---|---|
| Binary Search Tree(이진 탐색 트리) (0) | 2025.02.20 |
| Tree (트리) (7) | 2024.10.03 |
| Circular Linked List(원형 연결 리스트) (Java) (2) | 2023.03.24 |
| Doubly Linked List(이중 연결 리스트) (Java) (0) | 2023.03.22 |

댓글